La fonction de production concerne la quantité maximale de production qui peut être obtenue à partir d’un nombre donné d’entrées. La fonction de production décrit une limite ou une frontière qui représente la limite de sortie pouvant être obtenue à partir de chaque combinaison possible d’entrées. Ainsi, la fonction de production donne des informations sur les augmentations et les diminutions des rendements d’échelle et sur les produits marginaux du travail et du capital.
La fonction production en économie
En économie, les rendements décroissants (également appelés rendement marginaux décroissants) correspondent à la diminution de la production marginale d’un processus de production lorsque la quantité d’un seul facteur de production augmente, tandis que les quantités de tous les autres facteurs de production restent constantes. La loi des rendements décroissants stipule que, dans tous les processus de production, ajouter plus d’un facteur de production tout en maintenant tous les autres constants produira à un moment donné des rendements par unité inférieurs. La loi des rendements décroissants n’implique pas que l’ajout d’un facteur supplémentaire réduira la production totale, une condition connue sous le nom de rendements négatifs, bien que cela soit courant.
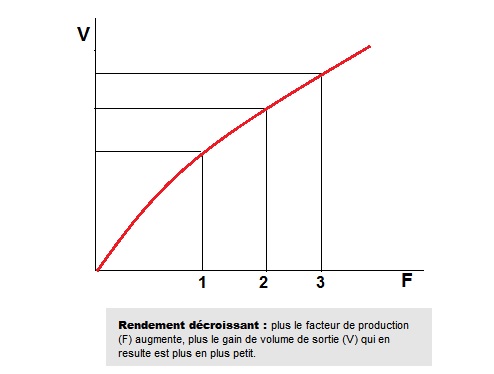
Par exemple, l’utilisation d’engrais améliore la production agricole dans les fermes et les jardins, mais à un moment donné, l’addition d’engrais améliore moins le rendement par unité d’engrais, et des quantités excessives peuvent même réduire le rendement. Un exemple courant consiste à ajouter plus de travailleurs à un travail, comme assembler une voiture dans un atelier. À un moment donné, l’ajout de plus de travailleurs provoque des problèmes tels que des travailleurs se gênant mutuellement ou se trouvant souvent en attente d’un accès à une pièce. Dans tous ces processus, la production d’une unité de production supplémentaire coûtera de plus en plus cher, du fait que les entrées sont de moins en moins utilisés.
Cette augmentation du coût marginal de la production lorsque la production augmente peut être représentée graphiquement par la courbe de coût marginal, avec la quantité de production sur l’axe des X et le coût marginal sur l’axe des Y. Pour de nombreuses entreprises, la courbe des coûts marginaux sera initialement inclinée vers le bas, ce qui représente une efficacité accrue à mesure que la production augmente.
Si la loi des rendements décroissants, la courbe des coûts marginaux finira par augmenter et continuer à augmenter, représentant des coûts marginaux de plus en plus élevés associés à une production supplémentaire.
Signification du fonction de production
En termes simples, la fonction de production fait référence à la relation fonctionnelle entre la quantité d’un bien produit (sortie) et les facteurs de production (entrées). De cette manière, la fonction de production reflète la production à laquelle nous pouvons nous attendre si nous avons tant de main-d’œuvre et tant de capital que de travail, etc.
En d’autres termes, on peut dire que la fonction de production est un indicateur de la relation physique entre les intrants et la production d’une entreprise. La raison derrière la relation physique est que les prix de l’argent n’y figurent pas. Cependant, il est ici essentiel de mentionner que, tout comme la fonction de la demande, une fonction de production est pour une période définie. Il montre le flux d’intrants résultant en un flux de sortie pendant un certain temps.
La fonction de production d’une entreprise dépend de l’état de la technologie. À chaque développement technologique, la fonction de production de l’entreprise évolue.
Comment calculer la fonction de production
Une fonction représente une relation entre deux variables. Par exemple, la variable X et la variable Y sont liées l’une à l’autre de telle sorte qu’un changement dans une variable entraîne un changement dans l’autre.La relation entre X et Y peut être montrée à l’aide d’une formule qui se représente comme suit:
- Y = F(x)
Dans la formule mentionnée, la valeur de Y peut être déterminée à l’aide de la valeur donnée de X. De même, dans la fonction de production est la représentation mathématique de la relation entre les entrées et les sorties d’une organisation. En d’autres termes, la fonction de production représente le rendement maximum qu’une organisation peut obtenir avec les combinaisons données de facteurs de production (terre, travail, capital et entreprise) au cours d’une période donnée avec la technologie donnée. Il s’agit d’un ensemble de différentes possibilités de production d’une organisation.
Fonction de production homogène linéaire
La fonction de production homogène linéaire implique qu’avec le changement proportionnel de tous les facteurs de production, la production augmente également dans la même proportion. Tels que, si les facteurs d’entrée sont doublés, la production devient également doublée. Ceci est également connu sous le nom de rendements constants à une échelle.
La fonction de production est dite homogène lorsque l’élasticité de substitution est égale à un. La fonction de production homogène linéaire peut être utilisée dans les études empiriques car elle peut être manipulée avec sagesse. Cette fonction de production peut être représentée symboliquement:
- nP : f (nK nL)
où, n = nombre de fois – nP = nombre d’augmentation de la production – nK = nombre d’augmentation du capital – nL = nombre d’augmentation du travail.
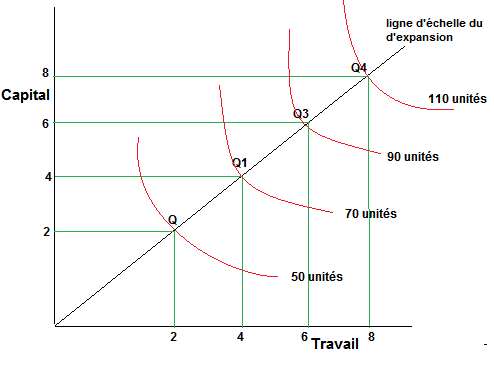
Dans le cas d’une fonction de production homogène linéaire, l’expansion est toujours une ligne droite passant par l’origine, comme le montre la figure. Cela signifie que les proportions entre les facteurs utilisés seront toujours les mêmes quel que soit le niveau de production, à condition que les prix des facteurs restent constants.
Conclusion
Voila un article en ligne sur la fonction de production. Merci d’avoir consulter notre article.